Miniaturization of voltage-controlled oscillators (VCOs) at lower microwave frequencies has long been limited by the size of the resonator. For the popular 4-to-8-GHz band, however, Synergy Microwave Corp. (Paterson, NJ) has managed to shrink multi-octave VCOs in that frequency range to a mere 0.3 x 0.3 in., with a companion line of frequency synthesizers that measure just 0.6 x 0.6 in. The discrete-device VCOs feature patented technology that achieves the high-stability and low-noise performance required for wideband, high-data-rate communications systems.1-8 They have been tested to 12 GHz and are available in tape-and-reel format for use with automated assembly equipment.
The new RoHS-compliant VCOs employ tiny planar resonators with a unique evanescentmode electromagnetic (EM) coupling mechanism for improved loaded quality factor (Q) and reduced phase noise. The current line of products is constructed with discrete components but the design approach lends itself to integrated-circuit (IC) formats using CMOS/BiCMOS/SiGe/GaAs technologies. The miniature VCOs can match the phase-noise performance of much larger, high-Q resonator-based oscillators and, because of their low mass, are relatively immune to high levels of shock and vibration.
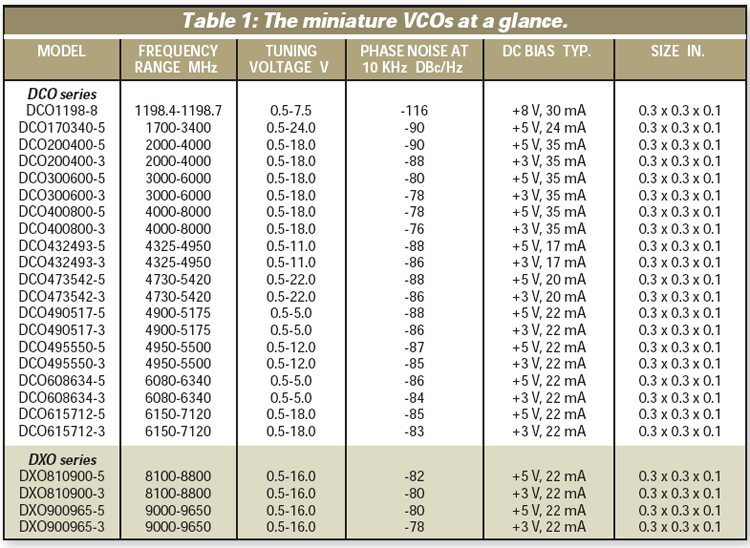
Because of the importance of wide bandwidth and low phase noise in modern systems, research into the development of the VCOs began with a study into ways of improving the firm’s innovative compact coupled planar resonator (CCPR) oscillators. Based on low-cost, printed coupled-resonatorbased designs, the new DCO and DXO series VCOs(Table 1) measure just 0.3 x 0.3 in. and can be used as building blocks in wideband frequency synthesizers measuring just 0.6 x 0.6 in.
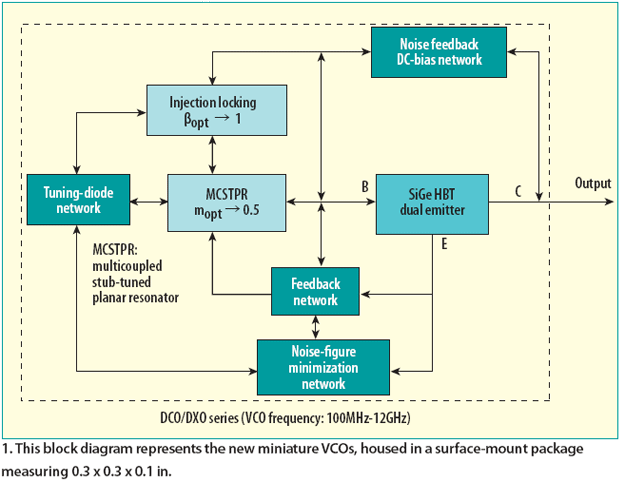
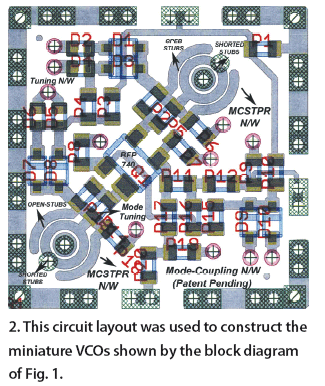
VCOs can be made small through the use of IC technology, although with sacrifices in tuning range and power consumption. Synergy’s approach in the new printed-circuit-resonator VCOs is a power-efficient fundamental-frequency solution that supports bandwidths as wide as 2:1 from 1 to 12 GHz. The new oscillators challenge the best IC VCOs and discrete SMD VCOs for given constraints of power consumption, tuning range, and cost. Figures 1 and 2 show the block diagram and layout for the DCO and DXO VCOs.
The new VCOs are designed for reliable performance from -40 to +85°C and are well suited for applications in industrial, military, and commercial systems. They employ a miniaturized multicoupled-stubs-tuned-planar-resonator (MCSTPR) approach, fabricated on low-loss 30-mil-thick dielectric material with dielectric constant of 3.38. The active device is a discrete low-noise silicon-germanium (SiGe) heterojunction- bipolar-transistor (HBT) device.
The VCOs are modeled by means of optimized nonlinear oscillator circuits simulated with two-and-one-halfdimension (2.5D) or three-dimensional (3D) electromagnetic (EM) simulation software. The nonlinear circuit model contains the oscillator’s active device, represented by its S-parameters. The HBT is modeled by large-signal S-parameters to better understand the behavior of the device under quasilinear (low-signal drive level) and nonlinear (large-signal drive level) conditions. This partitioning of the oscillator works quite well, and the combination of the S-parameters and the nonlinear circuit model agrees closely with measured data. This approach also improves the optimization cycles using harmonicbalance circuit simulators.
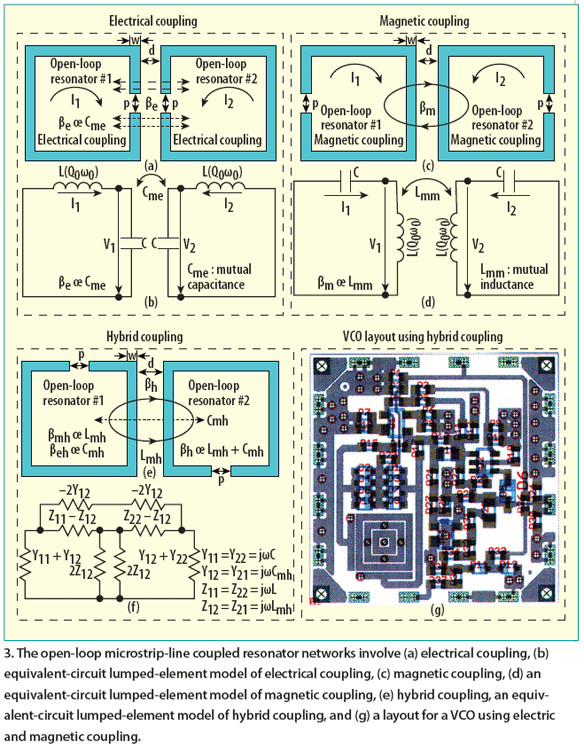
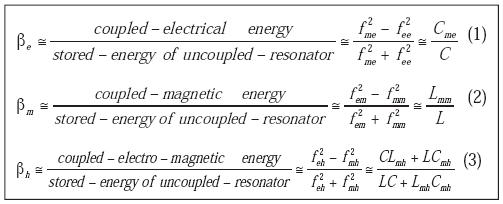
The quality factor (Q) of the coupled planar resonator network can be enhanced by introducing an optimum coupling mechanism (electric/magnetic/ hybrid). Figure 3 illustrates the layout of typical electric, magnetic, hybridcoupling planar resonator networks, and oscillator circuits for comparative analysis.9 The coupling dynamics can be characterized by proximity effect through the fringing fields, which decays exponentially outside the field region; the electric and magnetic field intensity tends to concentrate near the side having the maximum field distribution. The coupling factor ß (ße for the electric field, ßm for the magnetic field, and ßh for the hybrid field) are described in Eqs. 1-3. The loaded Q, QL, of the coupled resonator network is shown in Eqs. 4-8, given in terms of the unloaded Q, Qo.10 where
I = the rate of change of the phase and
QO = the unloaded Q-factor of the uncoupled single open loop microstrip resonator.
From Eqs. 6, 7, and 8, there is a trade off between improving the Q and the permissible attenuation required (which is compensated by active device for oscillation buildup). The coupling mechanism described in Figure 3 shows an improvement in Q in comparison to a single uncoupled planar resonator, although with a limited tuning range (less than 1 percent).
From Eqs. 6-8, the loaded Q (QL) can be maximized by either lowering the value of mutual capacitance (Cm) and inductance (Lm) or maximizing self-capacitance (C) and inductance (L). The upper limit of QL is dependent upon the coupling that can be optimized by controlling the width of the transmission line (w), the gap of the open line resonator (p), and the spacing between the two open line resonators (d). However, the dynamic control and tuning of parameters w, p, and d using IC technology at high frequencies is a challenging task.
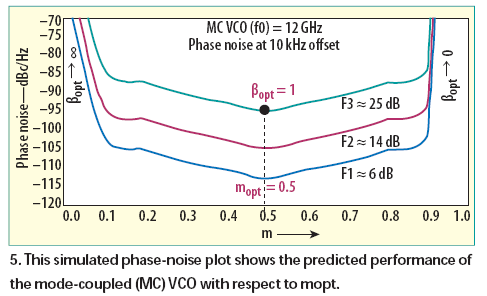
For wideband tunability, the coupling factor ßj must be dynamically tuned for low phase noise over the operating frequency band. A simplified approach for realization of dynamically controlled coupling factor ßj is by the use of a tuning diode as a coupling capacitor across the coupled resonator networks. The expression for phase noise can be given by Eqs. 9 and 10,10 where £(fm), fm, f0, fc, QL, Q0, F, k, T, Po, R, m, and K0 are the ratio of the sideband power in a 1-Hz bandwidth at fm to total power in dB, offset frequency, flicker corner frequency, loaded Q, unloaded Q, noise factor, Boltzman’s constant, temperature in degree Kelvin, average output power, equivalent noise resistance of tuning diode, ratio of the loaded and unloaded Q, and voltage gain, respectively. From Eqs. 6, 7, and 8, m is given in terms of coupling coefficient in Eq. 11. By differentiating Eq. 10 with respect to m and equating to zero, the local minimum value of phase noise for a given resonator and oscillator toplogy can be given by Eqs. 12 and 13. From Eq. 13, for low-phase-noise applications, mopt and ßopt should be dynamically tuned and must converge in the vicinity of mopt ˜ 0.5 and 0 < ßopt < 1, respectively, for best phase-noise performance.
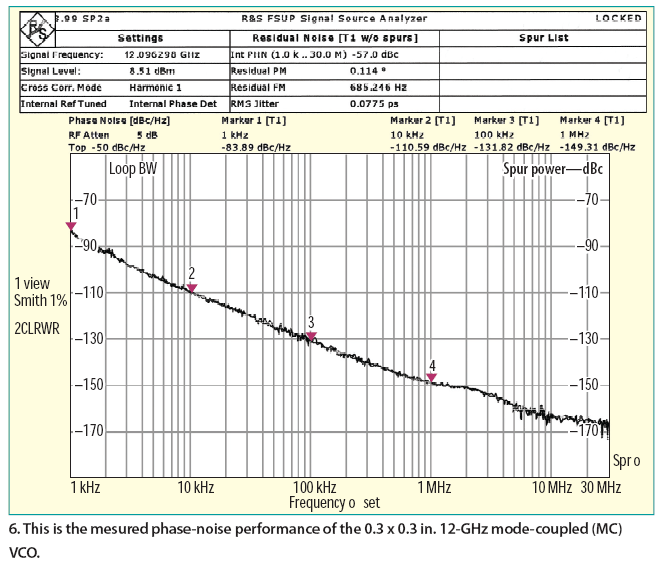
To validate the new VCO design approach (dynamically controlling mopt and ßopt for minimum noise figure), Fig. 4 shows the typical layout of a fixed-frequency, 12-GHz mode-coupled (MC) VCO based on a SiGe HBT device. It was fabricated on substrate material from Rogers Corp. with thickness of 30 mils and dielectric constant of 3.38. Figure 5 shows simulated phase noise for a 12-GHz mode-coupled (MC) VCO 10 kHz from the carrier with respect to mopt and ßopt. Figure 6 shows the measured phase noise of the discrete version.
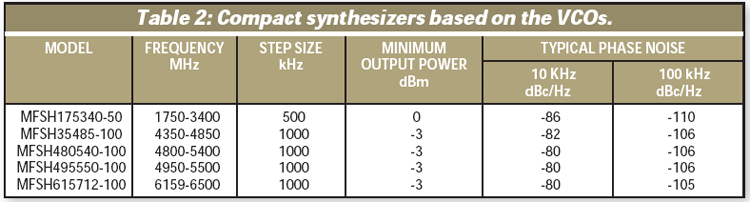
The VCOs were used to create the new MFSH series compact, configurable hybrid-type frequency synthesizers (Table 2), which measure just 0.6 x 0.6 in. in SMD packages.
For more information on the VCOs and/or synthesizers, contact Synergy Microwave or visit its web site.
Synergy Microwave Corp., 201 McLean Blvd., Paterson, NJ 07504; (973) 881- 8800, FAX: (973) 881-8361,
Internet: www.synergymwave.com.